Cấu trúc dữ liệu Đồ thị

Trong DSA Tags #giai-thuat #cau-truc-du-lieu #graph #algorithms #data-structure #do-thi Xuất bản 01/10/2021

Giới thiệu cấu trúc dữ liệu Đồ thị

Cấu trúc dữ liệu đồ thị là một tập hợp các nút có dữ liệu và được kết nối với các nút khác.

Hãy thử hiểu điều này thông qua một ví dụ. Trên facebook, mọi thứ đều là một nút. Điều đó bao gồm Người dùng, Ảnh, Album, Sự kiện, Nhóm, Trang, Bình luận, Câu chuyện, Video, Liên kết, Ghi chú ... bất cứ thứ gì có dữ liệu là một nút.

Mọi mối quan hệ là một cạnh từ nút này sang nút khác. Cho dù bạn đăng ảnh, tham gia nhóm, thích một trang, v.v., một lợi thế mới sẽ được tạo ra cho mối quan hệ đó. 

Tất cả facebook sau đó là một tập hợp của các nút và cạnh này. Điều này là do facebook sử dụng cấu trúc dữ liệu đồ thị để lưu trữ dữ liệu của nó.

Chính xác hơn, biểu đồ là một cấu trúc dữ liệu (V, E) bao gồm

  • Tập hợp các đỉnh V
  • Tập hợp các cạnh E, được biểu diễn dưới dạng các cặp đỉnh có thứ tự (u, v)

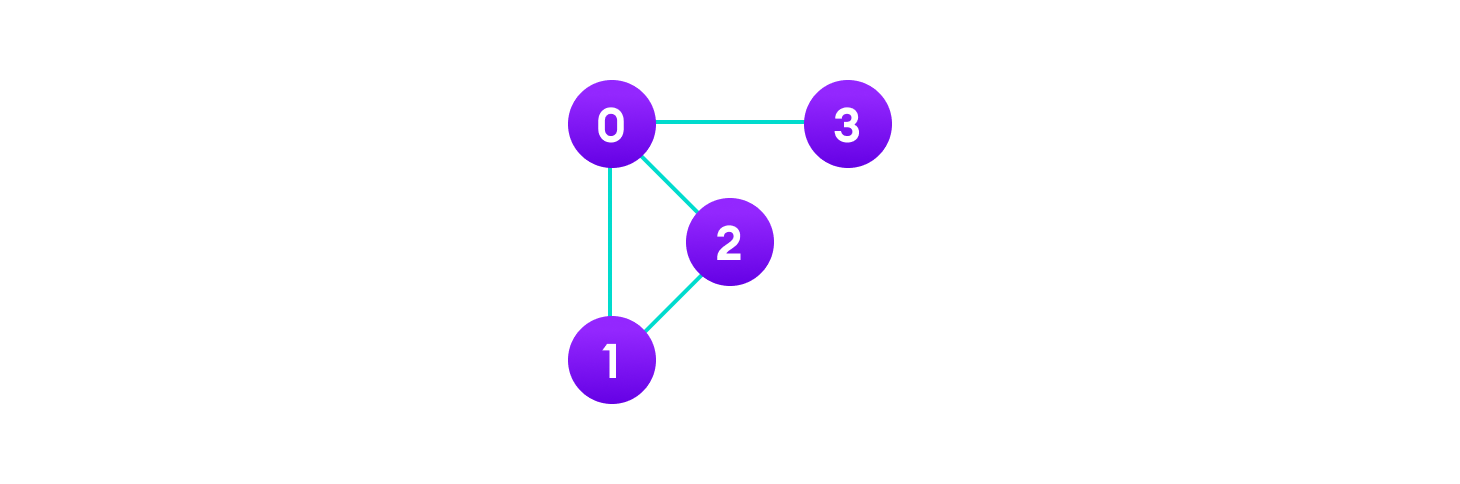
Trong đồ thị trên:

V = {0, 1, 2, 3}
E = {(0,1), (0,2), (0,3), (1,2)}
G = {V, E}

Các loại đồ thị

Đồ thị vô hướng

Trong đồ thị vô hướng, các nút được nối với nhau bằng các cạnh đều có hướng. Ví dụ: nếu một cạnh nối nút 1 và 2, chúng ta có thể đi ngang từ nút 1 đến nút 2 và từ nút 2 đến nút 1.

Đồ thị có hướng

Trong một đồ thị có hướng, các nút được nối với nhau bằng các cạnh có hướng - chúng chỉ đi theo một hướng. Ví dụ, nếu một cạnh nối nút 1 và 2, nhưng đầu mũi tên hướng về phía 2, chúng ta chỉ có thể đi ngang từ nút 1 đến nút 2 - không theo hướng ngược lại.

Đồ thị có trọng số

Đồ thị có trọng số là đồ thị mà mỗi cạnh có một giá trị được gọi là trọng số của cạnh.

Các thuật ngữ đồ thị

  • Đỉnh biểu diễn các đối tượng trong đồ thị, thường được đánh dấu bằng các số hoặc kí hiệu bằng các chữ cái in thường u,v,…
  • Liền kề (Adjacency): Một đỉnh được cho là kề với một đỉnh khác nếu có một cạnh nối chúng. Các đỉnh 2 và 3 không liền nhau vì không có cạnh giữa chúng
  • Cạnh nối đỉnh x với đỉnh y là một tập gồm hai phần tử x, y thường được vẽ dưới dạng một đoạn thẳng nối hai đỉnh
  • Cạnh có hướng (cung): Là một cặp đỉnh có thứ tự. Trong mỗi cặp có thứ tự đó, đỉnh thứ nhất được gọi là đỉnh đầu, đỉnh thứ hai là đỉnh cuối.
  • Cạnh vô hướng: Không quan tâm đến hướng và coi hai đỉnh như nhau.
  • Khuyên: Là một cạnh nối một đỉnh với chính nó.
  • Cạnh song song: Là hai cạnh cùng nối hai đỉnh u, v.
  • Đồ thị có hướng: Là đồ thị mà tất cả các cạnh trong đồ thị đều có hướng.
  • Đồ thị vô hướng: Là đồ thị mà tất cả các cạnh trong đồ thị đều vô hướng.
  • Đơn đồ thị: Là đồ thị không có khuyên và không có cạnh song song.
  • Đa đồ thị: Là đồ thị không phải là đơn đồ thị.
  • Bậc: Trong đồ thị vô hướng, bậc của đỉnh v trong đồ thị G, ký hiệu dG(u) là số cạnh liên thuộc với v, trong đó, khuyên được tính hai lần.
  • Đường đi và Chu trình:
    • Một dãy các đỉnh V = (v0,v1,…,vk) sao cho (vi-1, vI) ∊ E, ∀i: 1<=i<=k được gọi là một đường đi.
    • Một đường đi là chu trình khi v0 = vk.
  • Liên thông:
    • Một đồ thị vô hướng là liên thông nếu tồn tại đường đi giữa hai cặp đỉnh bất kì thuộc đồ thị.
    • Một đồ thị có hướng là liên thông nếu phiên bản vô hướng của đồ thị đó là liên thông.
  • Đồ thị phẳng là đồ thị có thể được vẽ trên mặt phẳng sao cho không có hai đỉnh nào trùng nhau và các cạnh nào trùng nhau hoặc cắt nhau.

Biểu diễn đồ thị

Đồ thị thông thường được biểu diễn bằng 2 cách:

  1. Ma trận kề
    • Ma trận kề là một mảng 2D gồm các đỉnh V x V. Mỗi hàng và cột đại diện cho một đỉnh.
    • Nếu giá trị của bất kỳ phần tử nào a[i][j] là 1, nó biểu thị rằng có một cạnh nối đỉnh i và đỉnh j.
    • Ma trận kề cho biểu đồ mà chúng tôi đã tạo ở trên là:
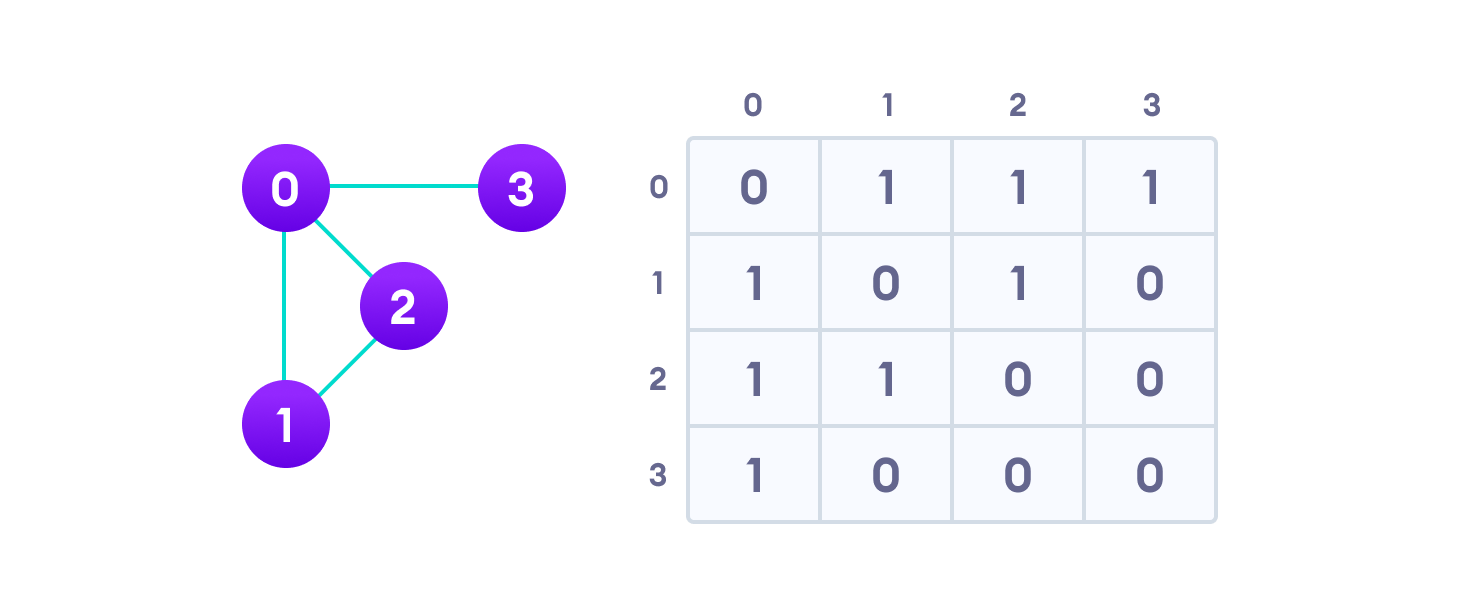
    • Vì là đồ thị vô hướng nên đối với cạnh (0,2), chúng ta cũng cần đánh dấu cạnh (2,0); làm cho ma trận kề đối xứng qua đường chéo.
    • Việc tra cứu cạnh (kiểm tra xem có tồn tại một cạnh giữa đỉnh A và đỉnh B hay không) là cực kỳ nhanh chóng trong biểu diễn ma trận kề nhưng chúng ta phải dành không gian cho mọi liên kết có thể có giữa tất cả các đỉnh (V x V), vì vậy nó đòi hỏi nhiều không gian hơn.
  2. Danh sách kề
    • Danh sách kề biểu thị một biểu đồ dưới dạng một mảng các danh sách được liên kết.
    • Chỉ số của mảng đại diện cho một đỉnh và mỗi phần tử trong danh sách liên kết của nó đại diện cho các đỉnh khác tạo thành một cạnh với đỉnh.
    • Danh sách kề cho biểu đồ mà chúng tôi đã tạo trong ví dụ đầu tiên như sau:
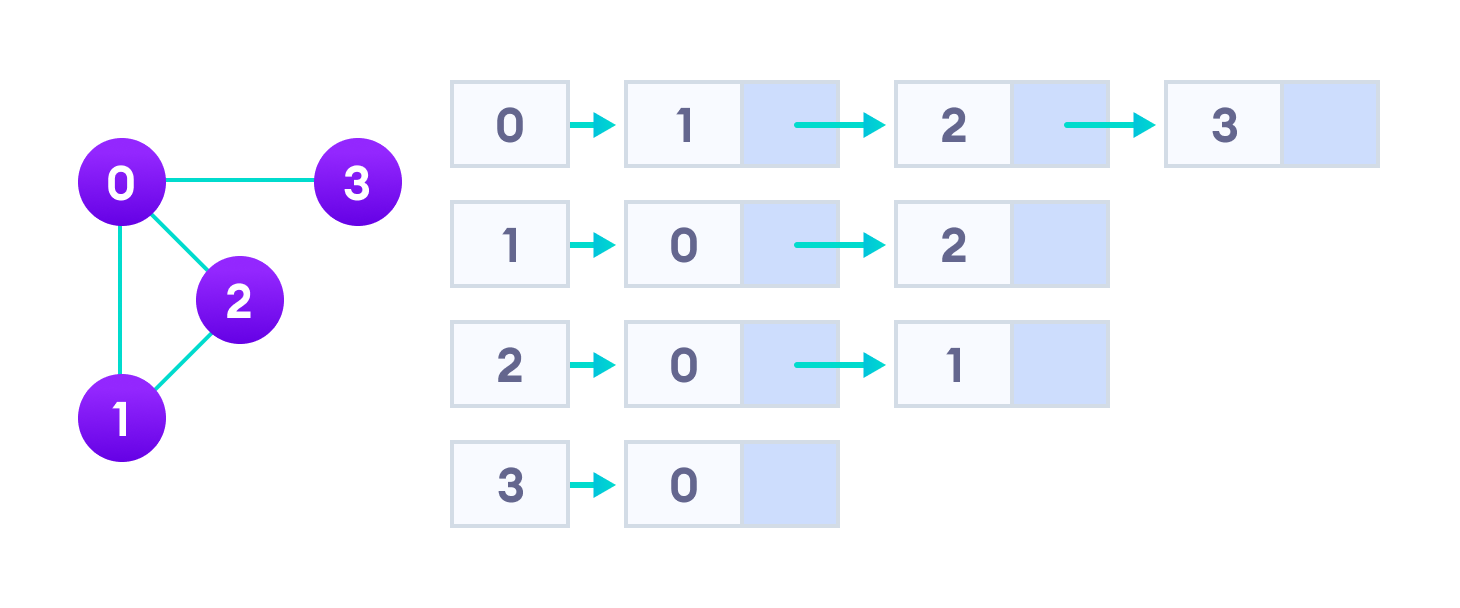
    • Danh sách kề là hiệu quả về mặt lưu trữ vì chúng ta chỉ cần lưu trữ các giá trị cho các cạnh. Đối với một đồ thị có hàng triệu đỉnh, điều này có nghĩa là rất nhiều không gian được tiết kiệm.

Các thao tác với Đồ thị

Các thao tác phổ biến nhất trên đồ thị là:

  • Kiểm tra xem phần tử có trong biểu đồ hay không
  • Duyệt đồ thị
  • Thêm các phần tử (đỉnh, cạnh) vào biểu đồ
  • Tìm đường đi từ đỉnh này sang đỉnh khác

Tài liệu tham khảo