Giải thuật đệ quy

Điều kiện cần:

Đã có kiến thức cơ bản về Cấu trúc dữ liệu và giải thuật

Giới thiệu về Giải thuật đệ quy

Trong khoa học máy tính, đệ quy là một phương pháp giải quyết một vấn đề trong đó giải pháp phụ thuộc vào các giải pháp cho các trường hợp nhỏ hơn của cùng một vấn đề. Những vấn đề như vậy thường có thể được giải quyết bằng cách lặp lại, nhưng điều này cần phải xác định và lập chỉ mục các trường hợp nhỏ hơn tại thời điểm lập trình. Đệ quy giải quyết các vấn đề đệ quy như vậy bằng cách sử dụng các hàm gọi chính hàm đó trong mã riêng của hàm. Cách tiếp cận này có thể được áp dụng cho nhiều dạng bài toán, và đệ quy là một trong những ý tưởng trung tâm của khoa học máy tính.

Sức mạnh của đệ quy rõ ràng nằm ở khả năng xác định một tập hợp vô hạn các đối tượng bằng một câu lệnh hữu hạn. Theo cách tương tự, một số lượng vô hạn các phép tính có thể được mô tả bằng một chương trình đệ quy hữu hạn, ngay cả khi chương trình này không chứa các lần lặp lại rõ ràng. Do vậy sử dụng giải thuật đệ quy thì một số vấn đề có thể được giải quyết dễ dàng.

Giải thích bằng toán học

Chúng ta hãy xem xét một bài toán mà một lập trình viên phải xác định giai thừa của số tự nhiên n, có một số cách để làm điều đó nhưng cách tiếp cận đơn giản nhất chỉ đơn giản là nhân các số bắt đầu từ 1 đến n. Vì vậy, hàm đơn giản trông giống như sau:

Giải pháp (1) - đơn giản nhân liên tục
     fact(n) = 1 * 2 * 3 * ... * n

nhưng có một cách tiếp cận toán học khác để thể hiện điều này:

Giải pháp (2) – Nhân đệ quy 
     fact(n) = 1               n=1
     fact(n) = n * fact(n-1)   n>1

Có một sự khác biệt đơn giản giữa Giải pháp (1) và Giải pháp (2) và đó là trong Giải pháp (2) bản thân hàm "fact()" đang được gọi bên trong hàm, vì vậy hiện tượng này được đặt tên là đệ quy và hàm chứa đệ quy được gọi là hàm đệ quy, nói chung đây là một công cụ tuyệt vời trong tay của các lập trình viên để viết mã một số vấn đề một cách dễ dàng và hiệu quả hơn rất nhiều.

Thực thi giải thuật đệ quy

Nhiều ngôn ngữ lập trình thực hiện đệ quy bằng các ngăn xếp. Nói chung, bất cứ khi nào một hàm nào gọi một hàm khác hoặc gọi chính nó, thì hàm gọi sẽ chuyển quyền điều khiển thực thi đến hàm được gọi. Quá trình chuyển này cũng có thể liên quan đến một số dữ liệu được chuyển từ hàm gọi đến hàm được gọi.

Điều này ngụ ý rằng, hàm người gọi phải tạm ngừng thực thi và tiếp tục lại sau khi điều khiển thực thi trả về từ hàm được gọi. Ở đây, hàm gọi cần phải bắt đầu chính xác từ thời điểm thực thi mà nó tự đặt nó ở trạng thái chờ. Nó cũng cần các giá trị dữ liệu chính xác giống như nó đã hoạt động. Với mục đích này, một bản ghi kích hoạt (hoặc khung ngăn xếp) được tạo cho hàm gọi.

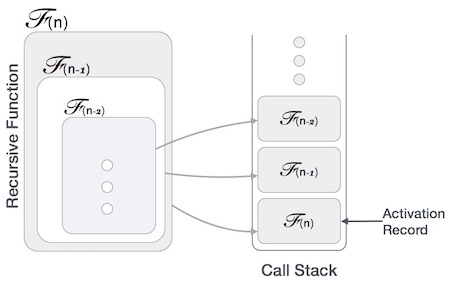
Bản ghi kích hoạt (Activation Recode) này lưu giữ thông tin về các biến cục bộ, các tham số chính thức, địa chỉ trả về và tất cả thông tin được chuyển đến hàm được gọi.

Tính chất Giải thuật đệ quy

Một hàm đệ quy có thể đi vô hạn giống như một vòng lặp. Để tránh chạy vô hạn hàm đệ quy, có hai thuộc tính mà một hàm đệ quy phải có:

Tiêu chí cơ sở - Phải có ít nhất một tiêu chí hoặc điều kiện cơ sở, sao cho khi điều kiện này được đáp ứng, hàm ngừng gọi chính nó một cách đệ quy.
Phương pháp tiếp cận lũy tiến - Các cuộc gọi đệ quy phải tiến triển theo cách mà mỗi khi một lệnh gọi đệ quy được thực hiện, nó lại gần với tiêu chí cơ sở hơn.

Tiêu chí cơ sở trong đệ quy là gì?

Trong chương trình đệ quy, lời giải cho trường hợp cơ sở được cung cấp và lời giải của bài toán lớn được thể hiện dưới dạng các bài toán nhỏ hơn.

Ví dụ:

int fact(int n){
  if(n<=1){
    return 1;
  }
  return n * fact(n-1);
}

Trong ví dụ trên, trường hợp cơ sở cho n <= 1 được xác định và giá trị lớn hơn của số có thể được giải quyết bằng cách chuyển đổi thành nhỏ hơn cho đến khi đạt được tiêu chí cơ sở.

Làm thế nào một vấn đề cụ thể được giải quyết bằng cách sử dụng đệ quy?

Ý tưởng là biểu diễn một vấn đề dưới dạng một hoặc nhiều vấn đề nhỏ hơn và thêm một hoặc nhiều tiêu chí cơ sở để dừng đệ quy. Ví dụ, chúng ta tính giai thừa n nếu chúng ta biết giai thừa của (n-1). Tiêu chí cơ sở cho giai thừa sẽ là n = 0. Chúng ta trả về 1 khi n = 0.

Tại sao có lỗi tràn (bộ nhớ) ngăn xếp (Stack Overflow) xảy ra trong đệ quy?

Nếu trường hợp cơ sở không đạt hoặc không được xác định, thì vấn đề tràn ngăn xếp có thể phát sinh. Hãy xem ví dụ để hiểu điều này:

int fact(int n){
    // wrong base case (it may cause stack overflow).
    if (n == 100) 
        return 1;
    return n*fact(n-1);
}

Nếu gọi fact(10) thì nó sẽ gọi là fact(9), fact(8), fact(7), ... nhưng con số sẽ không bao giờ đạt đến 100. Vì vậy, trường hợp cơ sở không đạt. Nếu bộ nhớ bị cạn kiệt bởi các chức năng này trên ngăn xếp, nó sẽ gây ra lỗi tràn ngăn xếp.

Phân tích giải thuật đệ quy

Có rất nhiều tranh luận tại sao phải sử dụng đệ quy, vì cùng một nhiệm vụ có thể được thực hiện với phép lặp. Lý do đầu tiên là, đệ quy làm cho một chương trình dễ đọc hơn và vì các hệ thống CPU nâng cao mới nhất, đệ quy hiệu quả hơn so với dùng vòng lặp.

Độ phức tạp thời gian

Trong trường hợp dùng vòng lặp, chúng ta lấy số lần lặp để đếm độ phức tạp về thời gian. Tương tự như vậy, trong trường hợp đệ quy, giả sử mọi thứ là không đổi, chúng ta cố gắng tìm ra số lần một lệnh gọi đệ quy được thực hiện. Một lệnh gọi hàm là Ο(1), do đó (n) số lần lệnh gọi đệ quy được thực hiện làm cho hàm đệ quy Ο(n).

Độ phức tạp không gian

Độ phức tạp của không gian được tính là lượng không gian bổ sung cần thiết để một mô-đun thực thi. Trong trường hợp dùng vòng lặp, trình biên dịch hầu như không yêu cầu thêm dung lượng. Trình biên dịch tiếp tục cập nhật giá trị của các biến được sử dụng trong các lần lặp. Nhưng trong trường hợp đệ quy, hệ thống cần lưu trữ bản ghi kích hoạt (Activation Record) mỗi khi thực hiện một lời gọi đệ quy. Do đó, có thể coi độ phức tạp không gian của hàm đệ quy có thể cao hơn so với hàm có lặp.