Kiến thức cần biết:
- Đã biết một ngôn ngữ lập trình
Khái niệm giải thuật (Algorithm)
Trong toán học và khoa học máy tính, giải thuật (hay thuật toán) là một chuỗi hữu hạn các chỉ dẫn cụ thể được xác định rõ, thường được sử dụng để giải một nhóm các vấn đề cụ thể hoặc để thực hiện một phép tính. Các giải thuật được sử dụng làm đặc tả để thực hiện tính toán, xử lý dữ liệu, suy luận tự động, ra quyết định tự động và các tác vụ khác. Ngược lại, phương pháp tiếp cận bằng cảm tính (heuristic) là một cách tiếp cận để giải quyết vấn đề có thể không được xác định đầy đủ hoặc có thể không đảm bảo kết quả chính xác hoặc tối ưu, đặc biệt trong các lĩnh vực vấn đề không có kết quả đúng hoặc tối ưu được xác định rõ ràng.
Giải thuật là một phương pháp hiệu quả, một thuật toán có thể được biểu diễn trong một khoảng không gian và thời gian hữu hạn, và bằng một ngôn ngữ hình thức được xác định rõ ràng để tính toán một hàm. Bắt đầu từ trạng thái ban đầu và đầu vào ban đầu (có thể trống), các lệnh mô tả một phép tính, khi được thực thi, sẽ tiến hành thông qua một số hữu hạn các trạng thái liên tiếp được xác định rõ, cuối cùng tạo ra "đầu ra" và kết thúc ở trạng thái kết thúc cuối cùng. Sự chuyển đổi từ trạng thái này sang trạng thái tiếp theo không nhất thiết phải mang tính xác định; một số thuật toán, được gọi là thuật toán ngẫu nhiên, kết hợp đầu vào ngẫu nhiên.
Giải thuật nói chung có thể tạo ra độc lập với ngôn ngữ tức là một giải thuật có thể thực thi trong nhiều ngôn ngữ lập trình.
Nếu bạn đang làm việc với các cấu trúc dữ liệu thì sẽ có phát sinh các loại giải thuật quan trọng sau:
- Tìm kiếm (Search) – Giải thuật tìm kiếm một phần tử trong cấu trúc dữ liệu.
- Sắp xếp (Sort) – Giải thuật để sắp xếp các phần tử trong cấu trúc dữ liệu theo một thứ tự nhất định.
- Chèn (Insert) – Giải thuật để chèn một phần tử vào trong một cấu trúc dữ liệu.
- Cập nhật (Update) – Giải thuật để cập nhật một phần tử đã tồn tại trong một cấu trúc dữ liệu.
- Xoá (Delete) − Giải thuật xoá một phần tử đã tồn tại trong một cấu trúc dữ liệu.
Các đặc điểm của một giải thuật
Không phải tất cả các thủ tục đều có thể gọi là giải thuật. Một giải thuật phải có các đặc điểm sau:
- Rõ ràng (Unambiguous) – Giải thuật phải dễ hiểu và rõ ràng. Với mỗi bước (hoặc giai đoạn) phải có đầu vào/ đầu ra phải dễ hiểu và phải gắn với một ý nghĩa nhất định.
- Đầu vào (Input) – Một giải thuật nên có 0 hoặc nhiều hơn một đầu vào được xác định rõ.
- Đầu ra (Output) – Một giải thuật nên có một hoặc nhiều hơn đầu ra được xác định rõ, và nên khớp với đầu ra mong muốn.
- Tính hữu hạn (Finiteness) – Giải thuật phải xác định giới hạn sau một số bước hữu hạn.
- Tính khả thi (Feasibility) – Nên khả thi với những tài nguyên có sẵn.
- Tính độc lập (Independent) – Một giải thuật nên điều kiển từng bước một, giải thuật nên độc lập với bất cứ mã lập trình nào.
Làm thế nào để viết một giải thuật?
Thật ra không có một chuẩn xác định nào để viết giải thuật. Đúng hơn là nó phụ thuộc vào vấn đề và tài nguyên. Giải thuật không bao giờ viết hỗ trợ cho một mã lệnh lập trình cụ thể nào.
Như chúng ta đã biết tất cả các ngôn ngữ lập trình đều có những cấu trúc cơ bản như vòng lặp (for, while, do), rẽ nhãnh (if-else)… Chúng ta có thể sử dụng các cấu trúc này để viết giải thuật.
Chúng ta viết giải thuật theo kiểu từng bước một nhưng không phải là tất cả các trường hợp. Giải thuật được viết là một quá trình và thực thi sau khi phạm vi vấn đề được xác định rõ ràng. Đó là chúng ta nên xác định phạm vi vấn đề sau đó mới đưa ra giải pháp.
Ví dụ về giải thuật Euclid
Lưu đồ thuật toán (thuật toán Euclid) để tính ước số chung lớn nhất (gcd) của hai số a và b ở các vị trí có tên A và B. Thuật toán tiến hành bằng các phép trừ liên tiếp trong hai vòng lặp: NẾU phép thử B ≥ A cho kết quả "yes" hoặc "true" (chính xác hơn là số b ở vị trí B lớn hơn hoặc bằng số a ở vị trí A) VẬY, thuật toán chỉ định B ← B - A (nghĩa là số b - a thay thế b cũ). Tương tự, IF A> B, THEN A ← A - B. Quá trình kết thúc khi (nội dung của) B bằng 0, mang lại g.c.d. ở A.
(Thuật toán lấy từ Scott 2009: 13; ký hiệu và phong cách vẽ từ Tausworthe 1977).
Phân tích giải thuật
Hiệu quả của một giải thuật có thể phân tích theo hai giai đoạn khác nhau, trước và sau khi thực thi.
- Phân tích tiên nghiệm (trước khi thực thi): Đây là một phân tích lý thuyết của giải thuật. Hiệu quả của giải thuật được đo bằng nhiều yếu tố khác nhau. Ví dụ tốc độ bộ vi xử lý là một hằng số và không ảnh hưởng đến quá trình thực thi.
- Phân tích hậu nghiệm (sau khi thực thi): Đây là một phân tích thực nghiệm của một giải thuật. Giải thuật được lựa chọn được thực hiện bằng cách sử dụng ngôn ngữ lập trình. Sau đó được thực hiện trên một máy tính xác định. Trong phân tích này, thống kê thực tế như thời gian chạy và yêu cầu không gian (bộ nhớ) được thu thập.
Chúng ta sẽ tìm hiểu về phân tích giải thuật tiên nghiệm. Phân tích giải thuật đề cập đến việc thực hiện hoặc thời gian chạy các thao tác liên quan. Thời gian chạy của một thao tác có thể định nghĩa là số lần máy thính thực hiện các chỉ thị trên một thao tác.
Sau đây chúng ta sẽ đi sâu vào việc phân tích thuật toán dựa theo:
- Độ phức tạp của giải thuật
Giả sử X là một giải thuật và n là kích thước dữ liệu đầu vào, thời gian và không gian (bộ nhớ) sử dụng bởi thuật toán X có 2 yếu tố ảnh hưởng đến hiệu quả của X:
- Yếu tố thời gian (Time Factor) − Thời gian được đo bằng cách đếm số lượng các thao tác chính như phép so sánh trong giải thuật sắp xếp.
- Yếu tố không gian (Space Factor) − Không gian được đo bằng cách tính không gian bộ nhớ tối đa cần thiết của thuật toán.
Sự phức tạp của một giải thuật f(n) cho phép thời gian chạy và / hoặc không gian lưu trữ theo yêu cầu của thuật toán với n là kích thước của dữ liệu đầu vào.
- Độ phức tạp không gian (bộ nhớ)
Độ phức tạp không gian của giải thuật biểu diễn số lượng không gian bộ nhớ cần thiết của giải thuật trong vòng đời của nó. Không gian cần thiết của giải thuật bằng tổng 2 thành phần sau:
- Một phần cố định là không gian cần thiết để lưu trữ dữ liệu và biến, nó độc lập với kích thước của vấn đề. Ví dụ: các biến đơn giản và các hằng số được sử dụng, kích cỡ của chương trình,…
- Một phần biến là không gian cần thiết lưu trữ biến, kích thước của nó phụ thuộc vào kích thước của vấn đề. Ví dụ: cấp phát bộ nhớ động, không gian ngăn xếp đệ quy,…
Độ phức tạp không gian S(P) của bất kỳ thuật toán P là S(P) = C + SP(I), trong đó C là phần cố định và S(I) là biến thành phần của giải thuật, nó phụ thuộc vào đặc trưng thể hiện của I.
- Độ phức tạp thời gian
Độ phức tạp thời gian của một giải thuật biểu diễn bằng số lượng thời gian cần thiết để chạy hoàn thành giải thuật. Thời gian cần thiết có thể định nghĩa bằng một hàm số học T(n), trong đó T(n) có thể được xác định số bước với mỗi bước tốn một hằng số thời gian.
Đánh giá hiệu quả của giải thuật - Phân tích tiệm cận
Phân tích tiệm cận của một giải thuật đề cập đến định nghĩa gianh giới/bộ khung của hiệu suất chạy. Sử dụng phân tích tiệm cận chúng ta có thể kết luận được trường hợp tốt nhất, trường hợp trung bình và trường hợp xấu nhất của một giải thuật.
Phân tích tiệm cận là đầu vào bị giới hạn, nghĩa là nếu không có đầu vào cho giải thuật thì nó sẽ làm việc trong một hằng số thời gian. Những yếu tố khác so với đầu vào được coi là hằng số.
Phân tích tiệm cận là đề cập đến tính toán thời gian chạy của bất kỳ thao tác nào theo đơn vị toán học. Ví dụ: thời gian chạy của một thao tác được tính là f(n) và một thao tác khác được tính là g(n2). Điều đó có nghĩa là thời gian chạy của thao tác đầu tiên sẽ tăng tuyến tính với n và thời gian chạy của thao thác thứ 2 sẽ tăng theo hàm mũ so với n. Cũng như vậy thời gian chạy của 2 thao tác trên sẽ như nhau nếu n nhỏ đáng kể.
Thông thường thời gian cần thiết chạy giải thuật rơi vào 3 loại sau:
- Trường hợp tốt nhất (Best Case) − Thời gian nhỏ nhất cần thiết để chạy chương trình.
- Trường hợp trung bình (Average Case) − Thời gian trung bình cần thiết để chạy chương trình.
- Trường hợp xấu nhất (Worst Case) − Thời gian tối đa cần thiết để chạy chương trình.
Các ký hiệu tiệm cận
Một vài ký hiệu tiệm cận thông dụng để tính toán độ phực tạp thời gian thực thi của một giải thuật:
- Ký hiệu Ο: Ký hiệu Ο(n) là cách thức tính cận trên của thời gian chạy giải thuật. Nó có nghĩa là trường hợp xấu nhất của độ phức tạp thời gian hay thời gian lâu nhất mà giải thuật có thể hoàn thành.
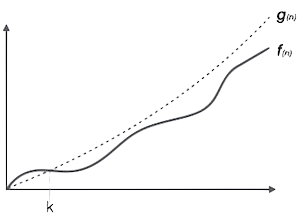
Ví dụ cho một hàm f(n)
Ο(f(n)) = { g(n) : tồn tại c > 0 và n0 thì f(n) ≤ c.g(n) với mọi n > n0. } - Ký hiệu Ω (Omega): Ký hiệu Ω(n) là các thức tính cận dưới của thời gian thực hiện giải thuât. Nó có nghĩa là trường hợp tốt nhất của độ phức tạp thời gian hoặc thời gian ngắn nhất mà giải thuật có thể hoàn thành.
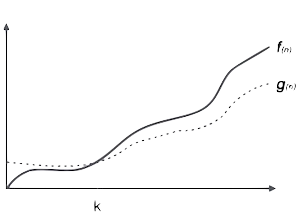
Ví dụ cho hàm f(n)
Ω(f(n)) = { g(n) : tồn tại c > 0 và n0 thì g(n) ≤ c.f(n) với mọi n > n0. } - Ký hiệu θ (Tê-ta): Ký hiệu θ(n) là cách tính cả hai cận trên và cận dưới của thời gian thực hiện giải thuật. Nó được biểu diễn như sau:
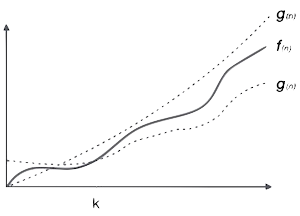
Ví dụ cho hàm f(n)
θ(f(n)) = { g(n) nếu và chỉ nếu g(n) = Ο(f(n)) và g(n) = Ω(f(n)) với mọi n > n0. }
Tính chất của một giải thuật tốt
- Đầu vào và đầu ra phải được xác định chính xác.
- Mỗi bước trong thuật toán phải rõ ràng và rõ ràng.
- Thuật toán nên hiệu quả nhất trong số nhiều cách khác nhau để giải quyết một vấn đề.
- Một thuật toán không được bao gồm mã máy tính. Thay vào đó, thuật toán nên được viết theo cách mà nó có thể được sử dụng trong các ngôn ngữ lập trình khác nhau.